nLab state monad
Context
Type theory
natural deduction metalanguage, practical foundations
type theory (dependent, intensional, observational type theory, homotopy type theory)
computational trinitarianism =
propositions as types +programs as proofs +relation type theory/category theory
Modalities, Closure and Reflection
Contents
Idea
The state monad is the name for the monad in computer science which is used to implement the functionality of read/write on a global “mutable state” (a global variable) in the context of functional programming languages.
A functional program with
-
output of type
-
and “mutable state” of type
(e.g. the state of a “random access memory” device, cf. Yates (2019), p. 26 & Fig. 1.10)
is clearly a function (morphism) of function type between the product types with (also known as a Mealy machine, see there and cf. Oliveira & Miraldo 2016, p. 462):
Now, under the hom-isomorphism of the (Cartesian product internal hom)-adjunction, this is equivalently given by its adjunct, which is a function into the function type (internal hom):
Here the operation is the monad on the type system which is induced by the above adjunction; and this latter function is naturally regarded as a morphism in the Kleisli category of this monad.
In the context of monads in computer science, this is called the state monad for mutable states of type , such as for a data type of Random-Access-Memory:

Definition
Concretely, with the underlying functor being
the join operation of the -state monad is given by evaluation on the intermediate -variable, hence the bind operation is given as follows:
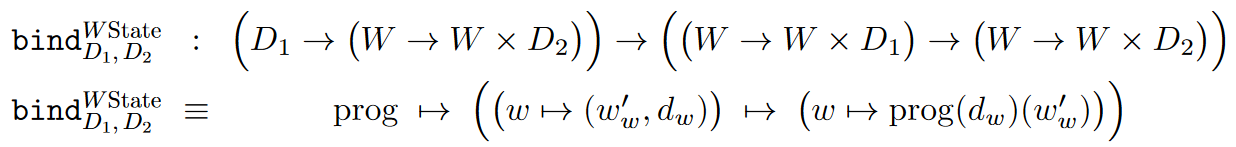
To see more in detail how this encodes access to a global variable in the sense of programming languages consider the following operations which isolate the processes of reading from and writing to that variable, respectively:
With these, for instance the procedure
which first reads-in the state of a global natural number variable and then overwrites it by its increment may be constructed as shown (on the right in do-notation) here:

(This is essentially the example from Benton, Hughes & Moggi 2002 p. 68 & 71)
Properties
Realization in dependent type theory
In a locally Cartesian closed category/dependent type theory , then to every type is associated its base change adjoint triple
In terms of this the state monad is the composite
of context extension followed by dependent sum, followed by context extension, followed by dependent product.
Here is called the function monad or reader monad and is the coreader comonad.
Related concepts
-
function monad (reader monad)
References
Original discussion of the state/side-effect monad as a monad in computer science:
-
Eugenio Moggi, Exp. 1.1 in: Notions of computation and monads, Information and Computation, 93 1 (1991) [doi:10.1016/0890-5401(91)90052-4, pdf]
-
Philip Wadler, Section 2.3 in: Monads for functional programming, in M. Broy (eds.) Program Design Calculi NATO ASI Series, 118 Springer (1992) [doi;10.1007/978-3-662-02880-3_8, pdf]
-
Nick Benton, John Hughes, Eugenio Moggi, Ex. 42 in: Monads and Effects, in: Applied Semantics, Lecture Notes in Computer Science 2395, Springer (2002) 42-122 [doi:10.1007/3-540-45699-6_2]
-
Gordon Plotkin, John Power, Section 3 of: Notions of computation determine monads In: M. Nielsen, U. Engberg, (eds.) FOSSACS 2002. LNCS, Lecture Notes in Computer Science 2303, Springer (2002) 342-356 [doi:10.1007/3-540-45931-6_24p]
Exposition:
- Bartosz Milewski, §21.2.5 in: Category Theory for Programmers, Blurb (2019) [pdf, github, webpage, ISBN:9780464243878]
On the modules (“algebras”) of the state monad:
- François Métayer, State monads and their algebras [arXiv:math/0407251]
Concrete applications via implementation in Haskell:
- Ryan Yates, Improving Haskell Transactional Memory (2019) [hdl:1802/35367, pdf]
Lecture notes:
- Tarmo Uustalu, p.24 of: Monads and Interaction Lecture 1 [pdf, pdf], lecture notes for MGS 2021 (2021):
In the generality of the local state monad:
-
Paul-André Melliès, Local States in String Diagrams, In: G. Dowek (eds.) Rewriting and Typed Lambda Calculi RTA TLCA 2014, Lecture Notes in Computer Science 8560, Springer (2014) [doi:10.1007/978-3-319-08918-8_23]
Explicit understanding of Kleisli morphisms for the state moand as Mealy machines:
- José Nuno Oliveira, Victor Cacciari Miraldo, p. 462 in: A practical approach to state-based system calculi, Journal of Logical and Algebraic Methods in Programming 85 4 (2016) 449-474 [doi:10.1016/j.jlamp.2015.11.007]
and (almost):
- Marco Perone, Georgios Karachalias, Composable Representable Executable Machines [arXiv:2307.09090]
Last revised on August 28, 2023 at 10:39:32. See the history of this page for a list of all contributions to it.